В последнее время (лето-осень 2017) на страницах Русской службы BBC примерно раз в неделю под рубрикой "Зарядка для ума" публикуются загадки. Но так ли эти они умны? Процитирую дословно две из них:
1. Какого цвета медведь? http://www.bbc.com/russian/other-news-41001479
Вы отправились на задание. Вы проехали 5 км на юг, затем 5 км на запад, затем 5 км на север и оказались в том же месте, откуда начали свой путь.
Во время своего путешествия вы видели медведя. Какого цвета он был?
2. Угадайте недостающее число. http://www.bbc.com/russian/other-news-41112029
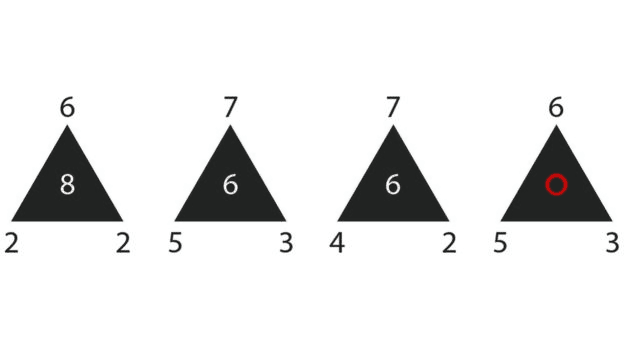
Какое число нужно вписать в пустой треугольник на картинке?

Теперь я скопирую с сайта BBC длинную картинку-заставку, которую они вставляют между задачей и её решением. Смысл этой картинки исключительно в том, чтобы дать читателю возможность поразмыслить немножко над задачей, а не прочесть случайно ответ сходу, по инерции.
После картинки я приведу ответы на эти 2 загадки и расскажу, что же с ними не так.

Вот какие ответы предлагает РС BBC, ссылаясь на авторов этих задач:
1. Белый
2. 3
Вот как они объясняют решение, цитирую также дословно:
1. Единственное место на Земле, где вы можете проехать 5 км на юг, затем 5 на запад, затем 5 на север и оказаться там, откуда вы отправились в путь, это Северный полюс.
На Северном полюсе обитают только полярные мишки, а они белого цвета.
2. Если из числа над треугольником вычесть число слева от него и умножить на число справа от треугольника, то получится число внутри него.
Вот, что с этими задачами не так:
1. Северный полюс - не единственное место, проделав от которого равные пути сначала на юг, затем на запад и затем на север, Вы окажетесь в точке старта. Даже если принять глагол "проехать" из условия задачи, как непременное требование находиться всё время на поверхности Земли (а не, допустим, в её центре, где понятия "Запад" попросту не существует), найдётся ещё бесконечное количество мест, в которых первая часть условия выполняется. Возьмите любую точку, удалённую от Южного - не от Северного, а именно от Южного полюса - на те самые 5 км плюс ещё 5/2πN км, где π - это число Пи, а N - любое целое число. Проехав из этой точки 5 км на юг, мы окажемся в точке на параллели длиной 5/N км, 5-километровое путешествие по которой через ровно N витков вокруг полюса вернёт нас в эту же точку, а ещё 5 км на север - в точку старта.
Что? В Антарктиде медведи не водятся? Вообще никакие? Не беда! В условии же не сказано, что мы живьём встретили медведя и непременно дикого. Там сказано "увидели". Увидеть можно любого медведя и где угодно, его даже не обязательно туда привозить, достаточно вытащить из кармана его фотку.
И вот какой урок из этого следует извлечь тому, кто хочет сочинять хорошие задачи: необходим тщательно выверенный баланс между слишком расплывчатым условием, допускающим различные толкования, т.е., различные решения и условием слишком жёстким и подробным, поскольку в таком решении внимательный читатель углядит подсказку, резко упрощающую задачу.
2. Существует ещё бесконечное количество функций таких, что f(6,2,2)=8; f(7,5,3)=6 и f(7,4,2)=6. Вот одна из них: f(a,b,c)=(a%2)*3*(b-c)+((a+1)%2)*2*(b+c), где "%" - операция "Остаток от деления". Говоря текстом, если верхнее число чётное, то берём удвоенную сумму нижних чисел, а если нечётное - то их утроенную сумму.
И да, эта функция для четвёртого треугольника даст отнюдь не 3, а ажно 16. В условии же не было сказано "цифра", там было сказано "число", а число имеет полное право быть двузначным.
Впрочем, даже будь в условии сказано "цифра", а не "число", это не спасло бы автора от решения, предложенного в комментариях Николаем Лисенко: сумма верхнего ряда цифр - 26, сумма нижнего ряда - 26, значит, сумма цифр внутри треугольников тоже должна равняться 26, а значит, искомое число - 6.
Второй урок таков: избегайте задач на поиск закономерностей в числовых рядах, т.к. вам самим может не хватить ни времени, ни познаний в математике на то, чтобы сформулировать условие достаточно жёстко.
И вот вам третий урок: мы все, надеюсь, знаем, что у любой сколь угодно сложной задачи есть простое и интуитивно-понятное неправильное решение. Но многие постоянно забывают о том, что найденное простое решение, даже если оно правильное, может оказаться не единственным правильным решением.
...поскольку, задавая их другим, очень легко нарваться на умника, который станет доказывать Вам, знающему Правильный Ответ, что решение у головоломки совершенно иное. И таки докажет.
Эта часть - о решении головоломок на поиск закономерностей в наборах чисел.
Опубликовав пост "Неправильные задачи" на Пикабу, я подчеркнул, что задача с треугольниками некорректна потому, что у неё бесконечное количество решений, любое из которых можно, не нарушая её условий, объявить "правильным".
Дальнейшие пикабушные комменты показали, что решений действительно много. В частности, было обосновано, что в четвёртый треугольник можно вписать не только 3, как предлагают нам авторы задачи в ответе, но и 4, и 6, и даже 16.
Сейчас я сначала найду самое математически-простое решение, а затем с вашей помощью докажу, что в 4-й треугольник можно вписать вообще любое число, хоть стопицот, да не просто вписать, а ещё и обосновать это, как найденную некую закономерность.
Существует универсальный алгоритм, решающий любую задачу типа "Каким образом из трёх чисел получилось четвёртое?", или, в более общем случае, "Каким образом из N чисел получилось N+первое?", если в условии дано не более N комплектов по N чисел.
Назовём это самое "Каким образом?" некой функцией от N аргументов, в нашем случае от 3. И запишем эту функцию, например, в виде следующего ряда:
f(x,y,z) = Axyz + Bxy + Cxz + Dyz + Ex + Fy + Gz
Вообще, ряд может быть и сложнее, с квадратами чисел, с их кубами, с логарифмами и прочим тяжёлым матаном, но в нашем конкретном случае даже и такого ряда многовато:
24A + 12B + 12C + 4D + 6E + 2F + 2G = 8
105A + 35B + 21C + 15D + 7E + 5F + 3G = 6
56A + 28B + 14C + 8D + 7E + 4F + 2G = 6
Система из 3 уравнений с 7 неизвестными. Куда нам столько?! Одно дело, когда компьютер под рукой и есть навыки программирования хотя бы на джаваскрипте. Тогда можно тупо с шагом 1 (исходя из того, что если это загадка, то коэффициенты наверняка целочисленные и небольшие) перебрать, допустим, 10000000 комбинаций значений A,B,C,D,E,F,G от -4 до 5 каждое и таким образом найти все варианты, включая вариант авторов задачи: C=1, D=-1, остальные нули. А как быть, если компьютера под рукой нет?
Линейная алгебра учит нас, что система из 3 линейно-независимых уравнений даёт единственное решение для 3 переменных, а если переменных больше, то число решений бесконечно. Мы можем вписать любые числа на место A,B,C и D, лишь бы только после этого уравнения оставались линейно-независимыми, то есть, не получаемыми друг из друга тупым умножением на какие-то числа, а затем сложением друг с другом.
Итак, поскольку нас устраивает любое из бесконечного множества решений, то зануляем сгоряча введённые члены уравнений (A=B=C=D=0) и получаем упрощённую систему из 3 уравнений с 3 неизвестными, которая должна иметь единственное решение:
6E + 2F + 2G = 8
7E + 5F + 3G = 6
7E + 4F + 2G = 6
Есть много способов аналитического решения систем линейных уравнений, самый элегантный, на мой взгляд, из них - матричный, но линейку учили не все, так что мы будем решать примитивным школьным способом.
Домножаем первое уравнение на коэффициент при E второго (он же и третьего), а второе и третье уравнения домножаем на коэффициент при первом E:
42E + 14F + 14G = 56
42E + 30F + 18G = 36
42E + 24F + 12G = 36
Вычитаем первое уравнение из двух оставшихся:
16F + 4G = -20
10F - 2G = -20
Домножаем теперь-второе уравнение на -2:
16F + 4G = -20
-20F + 4G = 40
Вычитаем из него теперь-первое:
-36F = 60
И получаем F = -60/36 = -5/3.
Теперь, определив F, можем решить любое из наших уравнений с двумя переменными:
16*(-5/3) + 4G = -20
-80/3 + 4G = -60/3, 4G = 20/3, G=5/3.
Чоза нафиг? G=-F? А ну-ка, проверим подстановкой в другое наше двухпеременное уравнение:
16*(-5/3) + 4*(5/3) = (-80+20)/3 = -20 таки да.
Наконец, имея коэффициенты F и G, находим из любого трёхпеременного уравнения коэффициент E. Например, из самого-самого первого:
6E + 2*(-5/3) + 2*5/3 = 8
6E = 8, E=4/3.
Функция найдена! f(x,y,z) = (4/3)x-(5/3)y+(5/3)z. Проверим её на втором и третьем треугольниках:
7*4/3 - 5*5/3 + 3*5/3 = (28-25+15)/3 = 18/3 = 6, сошлось!
7*4/3 - 4*5/3 + 2*5/3 = (28-20+10)/3 = 18/3 = 6, тоже сошлось!
И теперь нагло считаем по этой функции число, которое следует записать в четвёртый треугольник:
6*4/3 - 5*5/3 + 3*5/3 = (24-25+15)/3 = 14/3. Не целое? А нам какое дело! Формально задача решена, все свободны.
А Вас, уважаемый продвинутый Матано-Ботано, попрошу остаться.
Используя прочитанный Вами материал, найдите пожалуйста любое целочисленное решение задачи кроме авторского "xz-yz=3". Например, такое, при котором в четвёртый треугольник следует вписать круглый ноль.